Математика

Работы: Все Избранные В помощь учителю Конкурс «Учебный проект» Учебный год: Все 2015 / 2016 2014 / 2015 2013 / 2014 2012 / 2013 2011 / 2012 2010 / 2011 2009 / 2010 2008 / 2009 2007 / 2008 2006 / 2007 2005 / 2006 Сортировка: По алфавиту По новизне

• Презентация по теме "Теорема Пифагора"

  Работа знакомит с различными способами доказательства теоремы Пифагора.

• Прекрасные женщины — математики

  В наше время уже никого не удивляет тот факт, что многие представительницы "слабого пола" занимаются математикой. Но так было не всегда. Многие женщины с огромными трудностями пробивались к математике, преодолевая общественное непонимание, дикие законы и запреты, часто жертвуя личным благополучием, семейным счастьем. На страницах нашей работы мы разместили краткие рассказы о женщинах-подвижницах, об их деятельности и жизненном пути.

• Прекрасный мир фракталов

  Объектом исследования является молодая наука – фрактальная математика. На примере фракталов автор доказывает, что математика — развивающаяся наука, показывает связь математики с другими науками, а также создает свой собственный фрактал.

• Преобразование выражений, содержащих обратные тригонометрические функции

  Изучение тригонометрических уравнений базируется на знании обратных тригонометрических функций. Поэтому обучающиеся сначала детально прорабатывают понятия арксинуса, арккосинуса, арктангенса, арккотангенса, а затем только приступают к работе с синусом, косинусом, тангенсом и котангенсом.

• Преобразование графика квадратичной функции

  В работе, выполненной в виде презентации, представлены различные преобразования графика квадратичной функции.

• Преобразование графиков

  Презентация содержит наглядное представление о преобразовании графиков: сжатие, растяжение, параллельный перенос вдоль осей, сложение и вычитание.

• Преобразование графиков функции

  Рассмотрены преобразования графиков функций: параллельный перенос, осевая симметрия, сжатие и растяжение вдоль оси Y для различных функций, изучаемых в девятом классе. Работа представлена в виде презентации.

• Преобразование графиков функций

  

  Программа является электронным тренажером по теме "Преобразование графиков функций", который можно использовать при изучении нового материала, самоконтроля на уроках алгебры в средней школе (7-9-е классы). Представлены три функции: линейная, квадратичная и кубическая. Тренажер может использоваться и при повторении материала в старшей школе.

• Преобразование инверсии

  В работе рассматривается одно из неприменяемых геометрических преобразований плоскости – инверсия. Определены основные свойства (с построениями) инверсии, а также решён ряд конструктивных задач методом инверсии. Показано конкретное практическое приложение данного метода к задачам преобразования вращательного движения в прямолинейное.

• Преобразование Наполеона многоугольников

  

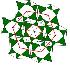
  Работа посвящена преобразованию Наполеона из множества n-угольников в себя. Работа содержит интересные результаты при n=3 и n=6. Кроме того, рассмотрен отдельный класс шестиугольников; дано полное геометрическое описание шестиугольников, преобразование которых вырожденное. Также сформулирована теорема, описывающая множество шестиугольников, являющихся преобразованием Наполеона исходных шестиугольников.

• Преобразование Наполеона четырехугольников

  

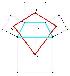
  Работа посвящена преобразованиям Наполеона четырехугольников, их интересным свойствам. Работа содержит экспериментальные доказательства этих свойств. Все исследования выполнены в среде "Живая математика". Кроме того, рассмотрено доказательство одного из свойств преобразования Наполеона четырехугольников.

• Преобразование пространства с помощью техники "Оригами"

  В работе представлен личный опыт автора – Владимира Иваницкого по изготовлению объемных фигур с помощью техники "Оригами", с последовательным описанием геометрических характеристик, математических рассчетов, а также технологических особенностей сборки этих фигур. В Приложении к работе представлен фоторепортаж, в котором отображены все фигуры, выполненные автором.

• Преобразование рисунков на координатной плоскости

  

  Работа знакомит с осевой симметрией, центральной симметрией, параллельным переносом, поворотом и гомотетией. Также приведена краткая биография великого математика Мишеля Шаль и сборник рисунков, придуманных автором.

• Преобразование тригонометрических функций

  Проект содержит красочные иллюстрации с изложением материала по теме "Преобразование тригонометрических функций" (алгебра, 10-й класс). Это поможет учащимся проследить за преобразованиями графиков функций. Работа способствует наиболее полному усвоению материала по данной теме.

• Преобразования графиков функции

  Построение графиков функций — одна из интереснейших тем в школьной математике. Крупнейший математик нашего времени Израиль Моисеевич Гельфонд писал: "Процесс построения графиков является способом превращения формул и описаний в геометрические образы. Это — построение графиков — является средством увидеть формулы и функции и проследить, каким образом эти функции меняются. Такое умение видеть сразу и формулу, и её геометрическую интерпретацию — является важным не только для изучения математики, но и для других предметов. Это умение, которое остается с вами на всю жизнь, подобно умению ездить на велосипеде, печатать на машинке или водить машину».

• Преобразования графиков функций

  

  В работе рассмотрены различные преобразования графиков функций: сдвиги вдоль осей координат; растяжение и сжатие графиков вдоль осей; построение графиков, содержащих модуль. К работе сделана презентация, иллюстрирующая эти преобразования.

• Преобразования графиков функций

  

  Цель работы: изучение способов построения графиков функций с помощью различных преобразований. Особенность работы по математике состоит в том, что в ней проведено исследование с точки зрения информатики. Абсолютно все графики были построены с помощью программных средств: Microsoft Office Exсel, Open Office Calс и Wolfram Mathematica, что дало возможность провести их сравнительный анализ.

• Преобразования графиков функций

  

  Работа представляет собой оформленный в виде презентации урок алгебры в 10-м классе с физико-математическим уклоном. Содержит анимированное представление преобразований графиков функций (сдвигов, симметрии, растяжений, сжатий). Изложены общие идеи и рекомендации по применению рассмотренных преобразований. Работу можно использовать на уроках алгебры, начиная с 7-го класса, постепенно усложняя и функции, и преобразования.

• Преобразования графиков, содержащих модуль

  Целью работы является исследование возможности рационального построения графиков функций и уравнений, содержащих модуль, и использование этих знаний при решении задач с параметрами.

• Приближенное построение правильных многоугольников

  

  В работе рассмотрены способы приближенного построения правильных многоугольников с помощью циркуля и линейки. Для некоторых из них создана анимация с помощью программы "Живая геометрия".

• Приборы, инструменты и приспособления для вычислений

  

  В работе представлены характеристики приборов, инструментов и приспособлений для вычислений. Даётся их описание, рекомендации и инструкции по их использованию. Также дается небольшой исторический экскурс во времена их создания и краткие биографические справки о создателях.

• Привелегии числу 7

  В работе рассказывается о числе 7: где оно встречается в жизни, в мифологии, в литературе, в математике; что означает число 7 в нумерологии, какую роль оно играет в жизни человека.

• "Привилегии" числа 7

  В докладе раскрывается удивительный мир числа 7 и показываются его "привилегии", которые люди оставили за числом 7. Рассматриваются несколько аспектов роли семерки и ее значение в жизни.

• "Привилегии" числу "семь"

  У древних народов числам приписывались особые свойства, в них видели проявление действия потусторонних сил. В своей работе автор попыталась рассмотреть в нескольких аспектах "привилегии", которые люди оставили за числом "семь".

• Приглашение в теорию чисел

  Знания о числах накапливались в течение многих веков, порождая интерес к новым исследованиям. Цель моей работы: Познакомиться с одной из ветвей математики — теорией чисел. В своей работе я рассмотрела такие понятия, как фигурные, совершенные числа, алгоритм Евклида и др. Показала практическое применение этих знаний при показе арифметических фокусов, игр с числами, при решении олимпиадных задач и задач ГИА и ЕГЭ.

• Приемы быстрого решения задач по теме "Наибольшее и наименьшее значения функции"

  

  При нахождении наибольшего и наименьшего значений функции можно использовать приемы быстрого решения без использования производной для большинства заданий В15 ЕГЭ по математике, учитывая, что ответ без округления должен быть целым числом или конечной десятичной дробью. Поиски более коротких путей решения задач по математике во время ЕГЭ сократят время выполнения заданий В1-В15 и сэкономит время для решения более сложных задач.

• Приемы быстрого счета

  Шестиклассникам стало интересно, смогут ли они быстро считать в уме. Это оказалось возможным, если овладеть некоторыми приемами. Познакомьтесь с этими приемами и удивите своих знакомых умножением двузначных чисел в уме. Также учениками создан буклет со сведениями об известных вычислителях.

• Приемы быстрого счета

  Мы сочли полезным собрать в данной работе некоторые приемы быстрого счета, основанные на применении известных в 5-м классе свойств действий над натуральными числами. Данная информация поможет учащимся научиться выполнять быстрые расчеты в уме.

• Приёмы быстрого счета

  В наш век компьютерных технологий умение быстро и правильно производить в уме вычисления не утратило своей актуальности. Каждый культурный человек должен уметь не только быстро производить простые расчеты в уме, но и оценивать, находить и исправлять ошибки в результате бытовых вычислений. В работе рассматриваются специальные и общие приемы устного счета, которые помогут развить у учащихся интерес и внедрить приобретенные приемы в образовательный процесс для дальнейшего успешного обучения.

• Приемы быстрого счета

  В работе представлены некоторые приемы техники быстрого счета. Работа будет полезна и учителям, и учащимся, и выпускникам на экзамене, где не разрешается пользоваться калькулятором.