Математика

Работы: Все Избранные В помощь учителю Конкурс «Учебный проект» Учебный год: Все 2015 / 2016 2014 / 2015 2013 / 2014 2012 / 2013 2011 / 2012 2010 / 2011 2009 / 2010 2008 / 2009 2007 / 2008 2006 / 2007 2005 / 2006 Сортировка: По алфавиту По новизне

• Математическое моделирование закона Архимеда

  В работе рассматривается природа возникновения силы Архимеда, рассчитывается математически закон Архимеда.

• Математическое моделирование и его практическое применение

  В работе рассматривается вид математического моделирования — математическое вышивание. В программе GSP ("Живая геометрия") выполнены деления окружности на 6, 12, 24, 9, 18, 36 частей, построены разные виды астроид, кардиоида со всеми расчетами. Разработаны собственные схемы для вышивания изонитью. К работе прикреплено приложение GSP.

• Математическое моделирование как способ решения задая (проблем)

  В работе рассмотрено применение моделирования при решении задач, выполнена их систематизация с позиции целеполагания, также рассмотрено применение моделирования к решению различных видов задач.

• Математическое моделирование окружающей среды

  Целью данной работы является освещение проблем экологии, загрязнения окружающей среды, воды, почвы, влияние загрязнений на сложившиеся экосистемы, моделирование процессов происходящих в природе.
  
  Экологический кризис сегодня — это уже беда не какого-нибудь одного региона, страны, континента. Проблемы выживания последующих поколений все настойчивее овладевают умами и сердцами граждан Земли.
  Математика создает условия для развития умения давать количественную оценку состояния природных объектов и явлений, положительных и отрицательных последствий деятельности человека в природном и социальном окружении. Текстовые задачи позволяют раскрыть вопросы о среде обитания, заботы о ней, рациональном природопользовании, восстановлении и приумножении ее природных богатств.

• Математическое моделирование. Свойства функций

  Математические формулы — это удобный язык для изложения идей и методов математики. Сами же эти идеи и методы можно описать, используя привычные и наглядные образы из окружающей среды. В работе рассматриваются основные свойства функции, которые излагаются в доступной и увлекательной форме, с использованием пословиц.

• Математическое наследие Древней Руси

  В работе представлены факты, подтверждающие существование высокой математической культуры на Руси в древности. Проводится исследование действующего Славянского Ведического календаря.

• Математическое наследие Каюма Насыри

  Актуальность проекта заключается в том, что богатейшее литературно-научное наследие Каюма Насыри является бесценным даром в воспитании молодого поколения. Объектом исследования является математическое наследие Каюма Насыри. Цель проекта — обобщение и представление в определенной целостности математических взглядов Каюма Насыри.

• Математическое обоснование решения проблемы выбора профиля в условиях современной школы

  

  При выборе профиля образовательному учреждению приходится сталкиваться с проблемой разногласия между мнениями родителей, учащихся, учителей и администрации. Как в этом случае принять оптимальное решение, удовлетворяющее интересам всех сторон? В данной работе предприняты попытки решения проблемы выбора профиля с помощью методов математической статистики, разработаны методические рекомендации для администрации образовательного учреждения для принятия оптимального решения в данной ситуации.

• Математическое описание случайных явлений

  Работа выполнена в форме презентации, она содержит теоретический и практический материал по указанной теме.

• Математическое описание случайных явлений. Интерактивный решебник

  В формате Power Point в работе представлено решение всех задач шестой главы «Математическое описание случайных явлений» учебника Ю.Т. Тюрина, А.А. Макарова, И.Р. Высоцкого, И.В. Ященко «Теория вероятностей и статистика». Работа состоит из пяти частей. В первой части рассмотрены задачи пункта 26 «Элементарные события».

• Математическое пособие "Знакомство с десятичными дробями"

  Разработанное пособие предназначено для обучающихся 5-х классов при знакомстве с десятичными дробями. Благодаря этому пособию школьник узнает много интересного из истории возникновения десятичных дробей, получит содержательную шпаргалку, которую сможет применять при выполнении действий с дробями.

• Математическое прогнозирование

  В работе представлены результаты исследования, проведённого среди учащихся класса. Полученные статистические данные показаны в виде таблиц и диаграмм и проанализированы с помощью простейших числовых характеристик положения и рассеивания.

• Математическое путешествие в мир гармонии

  Вашему вниманию представлена творческая работа учащихся с элементами исследования, рассматривающая симметрию в окружающем нас мире.

• Математическое стихотворение "Луч, отрезок и прямая"

  

  Стихотворение помогает лучше усвоить понятия "луч", "отрезок" и "прямая", помогает запомнить, как их изобразить и как правильно записать их названия.

• Материалы для математического досуга

  В статье подобраны увлекательные математические факты и доказательства, которые будут интересны для любознательных школьников.

• Матрица до нашей эры (Пифагор и его тайны)

  Работа выполнена в виде презентации, в которой рассказывается о великом ученом, философе и математике Пифагоре. В работе мы попытались найти связь между учением Пифагора и "боевиком тысячелетия" "Матрица", поставленным по собственному сценарию братьями Вачовски.

• Матрицы

  В работе раскрываются основные понятия теории матриц и показано применение матриц при решении задач экономического характера.

• Матричная алгебра в экономике

  В данной работе содержится информация о самих матрицах, операциях над ними и на примерах показано, как можно решать экономические задачи при помощи матриц.

• Медиана и биссектриса

  В работе изложен необходимый теоретический материал по заявленной теме, выходящий за рамки школьной программы. Широко представлен спектр задач на вычисления, доказательство и построение, где знания свойств медианы и биссектрисы необходимы. Уровень сложности представленных задач достаточно высок. Это и олимпиадные задачи, и задачи ЕГЭ по математике 2006 года. Весь материал подробно изложен, снабжен необходимыми иллюстрациями и может быть полезен при подготовке к экзаменам по математике.

• Медианы треугольника и площади фигур

  

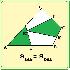
  В работе рассматривается хорошо известное свойство медианы треугольника – разделение его на два равновеликих треугольника. Опираясь на это основополагающее свойство медианы, автор обосновывает много интересных утверждений, причем делается это последовательно, по нарастающей трудности: от задач школьного учебника геометрии до задач олимпиадного уровня.

• Между математикой и искусством

  

  "Наука и искусство так же тесно связаны между собой, как сердце и легкое..." — писал Л.Н. Толстой. Цель этой работы — показать тесную связь между математикой и художественным искусством. В проекте представлено восемь тем. В каждой теме предложена научная теория вопроса и исследования в творческих работах автора.

• Международные меры объёма

  В работе представлены результаты изучения международных мер объёма, раскрыта история становления единой системы мер, приведены примеры мер объёма от Античности до наших дней.

• Межличностные отношения

  Тема охватывает практически весь диапазон отношений человека, начиная от его отношения к большим социальным группам (нации, рабочему коллективу) до интимных, диадных отношений (супружеских, отношений родитель – ребенок и т. д.).

• Межпредметные связи математики

  В работе показана значимость математических моделей для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования.

• Межпредметные связи экологии и математики. Математические задачи экологического содержания

  Экология — это емкая наука, которая имеет связи с любой школьной дисциплиной. В работе устанавливаются межпредметные связи экологии и математики на примере экологических математических задач. Подобраны примеры задач из учебников 5-6-го класса под редакцией Виленкина и 7-9-х классов под редакцией Теляковского.

• Межпредметный проект "Проверим алгеброй гармонию"

  В основе работы лежит раскрытие взаимосвязи науки и искусства, а также постижение многогранного мира художественных произведений, основанных на законах гармонии и красоты.

• Ментальные карты

  

  Работа представляет собой исследовательский проект. Она содержит информацию по теме "Ментальные карты", примеры ментальных карт, составленных авторами проекта, презентацию по данной теме. Авторы также составили памятку для всех желающих овладеть данным способом работы с информацией. Метод Тони Бьюзена на сегодняшний день один из самых эффективных и интересных методов, и каждый желающий может им овладеть.

• Мера времени

  Цель моей работы – изучить единицы времени, от первобытных до современных; познакомиться с создателями календарей, с изобретателями часовых механизмов, научиться определять и ценить своё время и время других людей. Проектными продуктами моего исследования будут: организация выставки «История создания меры времени» с последующим проведением экскурсии для ребят начальной школы; выпуск буклета для детей «А знаешь, как появилось время?», творческие работы учащихся: мини-проекты
  «Я моделирую часы».

• Меры длины

  В работе рассматриваются старинные и современные меры длины. Производится сравнение мер, перечислены пословицы и поговорки, в которых применяются старинные русские меры длины. Знание учащимися соотношения старинных русских мер и современных единиц измерения величин поможет легче понять содержание учебных и художественных текстов.

• Меры длины

  

  С тех пор как была принята единая метрическая система мер, старинные меры длины на практике не применяются. Но их нередко можно встретить в сказках, рассказах, книгах по истории, былинах. Со старинными мерами длины связано много фразеологизмов. Данная работа поможет представить, что значит выражение "от горшка два вершка", какого роста был Конёк-Горбунок и т.д.