Математика

Осевая симметрия

В работе дано определение осевой симметрии. Приведены примеры симметричных фигур в архитектуре, в изображениях человека, животных, различных предметов на фотографиях и в детских рисунках. Также рассмотрены примеры фигур, имеющих не одну ось симметрии.

Осевая симметрия в ненецких орнаментах

Рассмотрен способ построения ненецких орнаментов в компьютерной программе Power Point. Результатом исследования является методическая разработка по построению симметричных ненецких орнаментов при помощи программы Power Point, которая может быть использована не только учениками, но и преподавателями математики, технологии, родной литературы.

Осевая симметрия и построение графиков функций, содержащих модуль

В работе исследуются возможности использования осевой симметрии при построении графиков функций, содержащих модуль, приведены примеры построения графиков, представлена электронная версия построения графиков функций, созданная в MS PowerPoint с использованием анимации.

Основатели учения о золотом сечении

Цель исследования – систематизировать сведения об основоположниках учения о золотом сечении. Основателями учения о золотом сечении считаются знаменитые ученые, математики, архитекторы, художники, физики, алхимики, такие как Пифагор, Евклид, Леонардо да Винчи, Фибоначчи, Платон, Ле Корбюзье, Пачоли, Архимед, Гете, Дюрер и мн. др. И эти "великие" люди, заметившие это, передавшие это, – они поистине божественны!

Основные виды логических задач и методы их решения

В работе выделяются основные виды логических задач, рассматриваются наиболее удобные и простые методы решения, а также предлагается к рассмотрению известная задача Эйнштейна.

Основные методы построения сечений многогранников

В ЕГЭ 2010 года включены геометрические задачи практического содержания. Сегодня бессмысленно тратить время на рассуждение, отменят ЕГЭ или нет. Нужны конкретные мероприятия по развитию и укреплению знаний учащихся по геометрии. В работе представлены методы построения сечений на основе аксиом стереометрии, теорем о параллельности прямых и плоскостей. Особое внимание уделено методу следов, методу внутреннего проектирования и комбинированному методу.

Основные методы решения тригонометрических уравнений

Домашний репетитор подготовлен в рамках элективного курса для учащихся 11-го класса «Решение задач повышенной сложности по алгебре и началам анализа». Основная цель работы – познакомить учащихся с основными методами решения тригонометрических уравнений и способствовать формированию умения применять полученные знания к решению задач, выполнению творческих заданий. Используя учебное пособие, можно изучить теоретический курс по теме и оценить свои знания и навыки посредством прохождения теста.

Основные принципы криптографии и типы криптоанализа

Стремительное развитие информационных технологий оказывает существенное влияние на все стороны жизни государства и общества. Социальная, политическая, экономическая и военная сферы находятся в прямой зависимости от состояния защищенности информационной структуры России. Среди различных методов защиты информации особое место занимает криптография. Основным принципам криптографии и типам криптоанализа посвящена данная работа.

Основные углы в правильной пирамиде

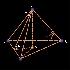
В работе установлены уравнения связи (формулы), с помощью которых можно определить угол наклона бокового ребра к плоскости основания правильной пирамиды, угол наклона боковой грани к плоскости основания, плоский угол при вершине пирамиды, двугранный угол при боковом ребре пирамиды, зная величину одного из углов.

Основные формулы алгебры

Содержание работы направлено на раскрытие важности формул сокращенного умножения при изучении математики. Цели проекта: показать важность формул сокращённого умножения и необходимость их использования в науке и на практике; провести исследование по качеству запоминания формул учащимися школы с 8-го по 11-й класс.

Основы сокрытия информации

Обоснована актуальность проблемы сокрытия информации в современном мире, рассказывается об истории криптографии, рассмотрены основные простейшие шифры, приведены фрагменты текстов из художественных произведений, в которых используются шифры. Рассматриваются задачи на дешифровку, самостоятельно решённые автором. Предложены простые рекомендации по эффективному хранению личной информации, приведены результаты анкетирования гимназистов.

Особенности записи числа 2 в двоичной системе счисления

В работе поставлена задача упрощения перевода больших чисел, представляющих собой число 2 в некоторой степени n, в двоичную систему счисления. Доказана теорема, с помощью которой скорость переводной операции увеличивается в сотни раз.

Особенности построения на клетчатой бумаге

Рассмотрены основные понятия при работе с клетчатой бумагой, проведено исследование возможностей бумаги в клетку при решении алгебраических и геометрических задач на построение.

Особенности социально-экономического развития малых городов на современном этапе

Мы хотим, чтобы наш посёлок развивался и когда-нибудь получил статус монопрофильного города. В работе мы предлагаем модель реструктуризации экономики моногородов, предприятий. Цель работы: определить эффективность методов управления развитием малых городов.

Остуол оонньуута "Торут куолгэ айан"

Бу сирдэрбит ?р сылларга чол туруктаах туралларыгар о5олуун-улаханныын бары кыhаллыахтаахпыт. Ол сыалтан, торообут дойдубут сирдэрин-уоттарын, уоскуур кыылларын-котордорун, булт быраабылаларын, сиэрин-туомун биhиги кыра эрдэхпититттэн билэр, ытыктыыр буолуохтаахпыт. Бэйэбит олорор сирдэрбит тустарынан литература суо5ун кэриэтэ. Ол иhин онорбут улэм улахан суолталаах дии саныыбын.

От абака до компьютера

Работа представляет собой краткий экскурс в историю вычислительной техники. Описаны древнейшие счетные приспособления — абаки, появившиеся около 2500 лет назад, современные вычислительные приборы. Рассказано о первооткрывателях механических счетных машин.

От арифметики к алгебре

Данная работа поможет в изучении истории пути от арифметики к алгебре на занятиях математического кружка.

От Евклида до Лобачевского

Авторами изучен и систематизирован материал, связанный с проблемой V постулата Евклида и поптытками доказать его математиками разных времен и народов. В работе сравниваются основные положения абсолютной и воображаемой геометрии, рассказывается о судьбе великого русского ученого Н.И. Лобачевского. Материал может быть использован на уроках и во внеклассной работе по математике. Имеется компьютерная презентация.

От игры к знаниям

Вашему вниманию представлены самодельные настольные математические игры, которые помогают детям лучше решать примеры и задачи в уме.

От натурального числа до мнимой единицы

История чисел поистине интереснейшая тема для изучения, ведь каждый день мы встречаемся с числами: с целыми, дробными, рациональными, натуральными. В работе, рассматривая эту тему, мы поставили перед собой ряд задач: рассказать об истории возникновения большинства существующих видов чисел, отдельно рассмотреть комплексные числа, выяснить, насколько они полезны, и найти их практическое применение.

От обыкновенных дробей к двоичным

В работе рассматриваются вопросы возникновения обыкновенных и десятичных дробей, способы их записи, применение, а также перевод десятичных дробей в двоичную систему счисления.

От отрезка до вектора

В работе предлагаются вопросы и задания в виде тестов, кроссвордов, чайнвордов. Эти задания направлены на активизацию учебной деятельности в процессе работы на уроке геометрии и во внеурочное время по этому предмету, на развитие мыслительных способностей учащихся и их эрудиции. Материал полностью соответствует действующим школьным программам.

От пальцев до калькулятора

В работе автор предлагает рассмотреть историю развития вычислительных средств в хронологической последовательности их изобретения.

От параллелограмма до золотого сечения

Работа освещает связь прямоугольника и золотой пропорции. Рассмотрены свойства прямоугольника в свете божественной пропорции, показаны способы построения и значение золотого сечения, примеры его в природе, применение в искусстве, архитектуре, являющееся непременным условием правильного и красивого изображения предмета. Очень интересна история возникновения и развития идеи золотой пропорции с IV в. до н.э.

От сложения до деления

Математика используется практически везде, но часто приходится производить очень большие вычисления или требуется быстро выполнить расчеты. На помощь людям пришли калькуляторы и компьютеры. Постепенно люди утрачивают навыки устного счета, уходят в прошлое различные способы и приемы вычислений. Цель работы: показать историческое развитие способов арифметических вычислений, выявить наиболее рациональные и удобные способы для быстрого счета.

От сферы к плоскости

Карты играют важную роль в жизни любого человека. Но как же переносят сферическую поверхность Земли на плоскость? Любое изображение фигур основано на так называемом проецировании, а само изображение пространственной фигуры на плоскости называют ее проекцией. Цель работы: найти математические правила, способы для проецирования изображений Земли на различные плоскости. В работе приводятся исторические сведения о глобусе; математические понятия, необходимые для работы с глобусом и картами; сравнивается градусная сетка глобуса и картографическая сетка карты; исследуются способы переноса глобуса на плоскость. В практической части выполнено изображение территории России и ХМАО в различных проекциях.

От счета на пальцах до персонального компьютера

Изучая исторические корни развития вычислительной техники, тем самым отвечаем на вопрос: какова причина отказа людей от счета на пальцах, показывая преимущества и многофункциональность персонального компьютера. На основе анкетирования разновозрастной аудитории проведен анализ исследования данной темы.

От чего зависит делимость чисел?

Предмет «Математика» многим ученикам нравится, но на деление многозначных чисел и числовых выражений требуется много времени, и поэтому встал вопрос: как быстро узнать на какое число можно разделить данное число, а на какое нет? Что надо знать такое, от чего зависит делимость чисел, числовых выражений? Это можно проверить, непосредственно выполняя деление в столбик или применяя признаки и свойства делимости.

Отбор корней в тригонометрических уравнениях и системах уравнений

В работе рассмотрены различные способы отбора корней в тригонометрических уравнениях: корни, удовлетворяющие неравенству, корни, принадлежащие промежутку. Изучены способы отбора корней уравнений, связанные с методом замены, а также содержащие дробные выражения, иррациональные выражения, уравнения с модулем, комбинированные уравнения. Подобраны задания для самостоятельного решения.

Ответы на вопросы к смотру знаний по геометрии

Представленная работа – это хорошая помощь при подготовке учащихся к ежегодному смотру знаний по геометрии, проводящемуся в нашей школе среди параллели 9-х классов в ноябре месяце. Работа содержит чертежи и краткие ответы по каждому из 78 вопросов.